Bowmain Consulting

Explicit Finite Differences

Part of Project Denning

This page contains several generations of code to value derivatives using explicit finite differences.

The First Generation

The first generation models the dimensionless version of the BS differential equation obtained by the well-known substitutions

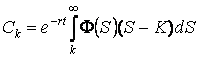
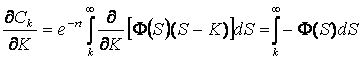
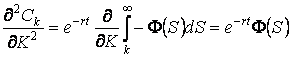
The resulting BS equation becomes the diffusion equation

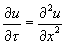Click here to download C++ and spreadsheet versions used to value a European put option. The LHS grid in the worksheet shows values calculated by explicit finite differences, the right hand side shows corresponding values calculated by BS.

Convergence

If N is the number of steps, the time taken to perform the calculations grows a N³.

D_m+1 ≤ (m+1)dt*(R₂dt + R₄(dx)²) ® 0 as dt ® 0, constant a, D_m+1 = difference between exact solution and finite difference value at t=t_m+1

Note (m+1)dt ® const, so convergence comes from R₂dt + R₄(dx)² term.

Comments

The following observations can be made about using the :

(1) Selection of the appropriate grid intervals is no longer intuitive. In the spreadsheet, 18 steps were used between S = 0.0001 and S=18. Even so, only the last row in a grid of 18 rows had S > 9.18. The result is that the interpolated values of the option at S=10 (strike) were significantly in error (approx 75% over-estimated). Since there is significant curvature of the value curve (gamma) at S = 10, the method will always under-estimates the value of the option at that point.

Accuracy could be improved by decreasing step size, but that probably represent a poor way to compensate for the exponential increase in step size as x increases.

It is tempting abandon the transformed equation and go back to modelling the BS equation directly. Wilmott [1] et. al. point out this leads to a separation of the criteria for stability an convergence, a potentially very dangerous state of affairs. For the moment, we heed the warnings.

Generally, practitioners are interested in values of an option around a specific value. A better solution (??) may be to choose K so that the gird has better coverage over the region of interest (K would no longer be the option strike) (HAVE NOT FULLY THOUGHT THIS THROUGH)

(2) The classic behaviour for a = dt/dx²> 0.5 can be seen with the C++ program by choosing a grid size with a = 0.5 and then decreasing the number of time steps (or increasing the number of x steps).

The Second Generation

References

1. "Option Pricing - Mathematical models and computation" by Paul Wilmott, Jeff Dewynne, Sam Howison.